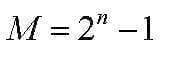Translation of information into binary code – what is it, its types, decoding

Everyone knows the ability of computers to calculate large groups of data in almost a matter of seconds. However, not everyone knows that this ability of electronic machines depends on the presence of current and voltage.

What is a binary code?

How does a computer manage to process huge amounts of information quickly? The binary system helps him in this. The data entering this smart device looks like ones and zeros. Each unit and each zero corresponds to a certain state of the electric wire:

• 1 – high voltage.
• 0 – low.

Or for units – the presence of voltage, and for zeros – the absence.

The basis of the binary system of calculation are binary codes. What is a binary code?

The process of converting data into zeros and ones is called "binary conversion", and their final designation is "binary code".

Bit depth of binary code

All binary numbers are a collection of bits, that is, ones and zeros, and each bit is one bit or one position in a binary number. Often in computer science tasks there is a question of how much information this or that binary code carries. You should know that each digit of the binary code contains the amount of information that is equal to one bit.

What is the bit depth of a binary code? If you look from the point of view of arithmetic, then the bit depth refers to the place that a digit occupies when writing numbers. Then, the bit depth of the binary code means the number of places of characters (digits) or the number of bits that are pre-allocated in order to write down the number.

Binary decryption

How to decrypt the binary code? The decimal notation is based on the decimal system that is commonly used in everyday life and the numerical values ​​here are represented as ten digits from zero to nine. Each of the places in the numbers is ten times more valuable than the place on the right. To represent a number greater than 9 in the decimal system, a zero is used, which is placed on the right. And the unit is located on the left in the next, more valuable place.

The binary system works in a similar way, in which only two digits are used – zero and one. Seats on the left are twice as valuable as seats on the right. So, for a binary code, it is typical that only 0 and 1 can be single numbers, and for any numbers greater than one, 2 places are already required.

After 0 and 1, the following binary numbers follow:

• 10 (that is, 1.0).
• 11 (1.1).
• 100(1,0,0).

In binary, 100 is the decimal equivalent of 4. Thus, any number can be expressed as a binary code, but it will take up more space. Also, by assigning certain binary numbers to each letter of the alphabet, any word can be translated into binary code.

Video about converting numbers to binary code

For example, to transmit a message over a digital communication channel, it is encoded, that is, each character of the original message is compared with a certain code (code word). For this, binary codes are used – a sequence of ones and zeros.

For example, to encode the word "mother" the following code is chosen:

• M – 00.
• A – 1.
• Y — 01.
• L — 0.
• U – 10.

Space is 11.

The encoded letters will be combined into one bit string and will be transmitted over the network in this form:

MOM SOAP LAMU → 0010011100010111010010

After this string has been delivered to its destination, the problem of restoring the original message must be solved. So, having received the message "001001", it can be decoded in several ways. For example, assuming that it consists only of the letters L (code 0) and A (code 1), you get:

LLALLAAALLLLALAAAALLALL

This means that the above code is not uniquely decodable. Uniquely decodable codes are those in which any code messages can be decoded in only one way.

Uniform codes

This problem is solved by properly splitting the bit string into separately encoded words. This can be done, for example, using a uniform code, the length of words in which is always the same. For example, this phrase consists of six characters, which means that a three-bit code can be applied.

For example, if you encode the above phrase with the following code:

• M – 000.
• A – 001.
• Y — 010.
• L — 011.
• Space – 101, then you get the following:

MOM SOAP LAMU → 000001000001101000010011001101011001000100

This message is 42 bits long. Although it is longer than the first one, which is only 22 bits, it is much easier to parse it into individual words for decoding:

000 001 000 001 101 000 010 011 001 101 011 001 000 100

M A M A M Y L A   L A M U 

Although such a uniform code cannot be called economical, it can be unambiguously decoded.

Video about converting letters to binary code

Uneven codes

Uneven binary code – what is it? It is sometimes used to shorten the length of messages. In a non-uniform code, the code word corresponding to a certain character in the alphabet may differ in length from other words.

For example, if you use the following code to encode "Mom soaped the llama":

• M – 01.
• A – 00.
• Y — 1011
• L — 100.
• U – 1010.
• Space – 11, it will turn out:

MOM SOAP LAMU → 0100010011011011100001110000011010

This message consists of 34 bits. This bit string can be decoded unambiguously, because in the first letter – M, which has code 01, the code is unique, because other code words do not start with 01. In the same way, you can determine the second letter – A. The property when the code words do not match the beginning other code words are called the Fano condition, and codes decoded using the Fano property are called prefix codes.

Prefix codes have an important practical meaning – with their help, the characters of received messages are decoded as they arrive, without waiting for the entire message to arrive at the recipient.

Types of binary codes

To represent integers, there are the following types of binary codes:

• Iconic.
• Unsigned.

Negative numbers can only be represented in signed form. Integers are stored in a computer in a fixed-point format.

Unsigned codes

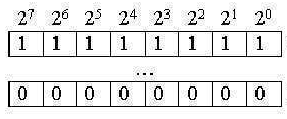
In integer unsigned binary codes, all binary digits are represented to the power of 2:

The value of the minimum possible number is zero, and the maximum is determined by the formula:

These two numbers define the range of numbers represented in binary code.

• If an eight-digit unsigned integer is presented, then the range of numbers is written using the code: 0…255.
• If a sixteen-digit code is presented – 0 … 65535.

In eight-bit processors, such numbers are stored in two memory cells, which are located in adjacent addresses. Working with such numbers is carried out using special commands.

Sign codes

In direct integer signed codes, the representation of the sign of a number is carried out using the most significant digit in the word. For a direct character code, zero is used to indicate the “+" sign, and one is used to indicate the “-” sign. Entering a sign bit will shift the range of numbers towards negative values.

• A binary eight-bit signed integer is written using the following range: -127…+127.
• The sixteen-digit code will be written in the range: -32767…+32767.

In eight-bit processors, such numbers are also stored in two memory cells, the addresses of which are located next to each other.

The disadvantage of this code is the need for separate processing of sign and digital bits. Programs running in such algorithms are quite complex. In order to select and change the sign bit, you will have to apply the bit masking method, which leads to an increase in the size of the program and a decrease in its performance. To prevent differences in the algorithm for processing digital and sign bits, reverse binary codes are used.

The difference between signed reverse binary codes and direct ones is the formation of negative numbers by inverting all bits of numbers. However, digital and sign bits do not differ. Such codes can significantly simplify the algorithm of work.

But, despite this, working with inverse codes requires a special algorithm in order to recognize signs, calculate the absolute values ​​of numbers, and restore the sign of the result of a number. Also, the direct reverse code of a number requires using two codes to remember zero at a time when it is known that zero is a positive number, and it can never be negative.